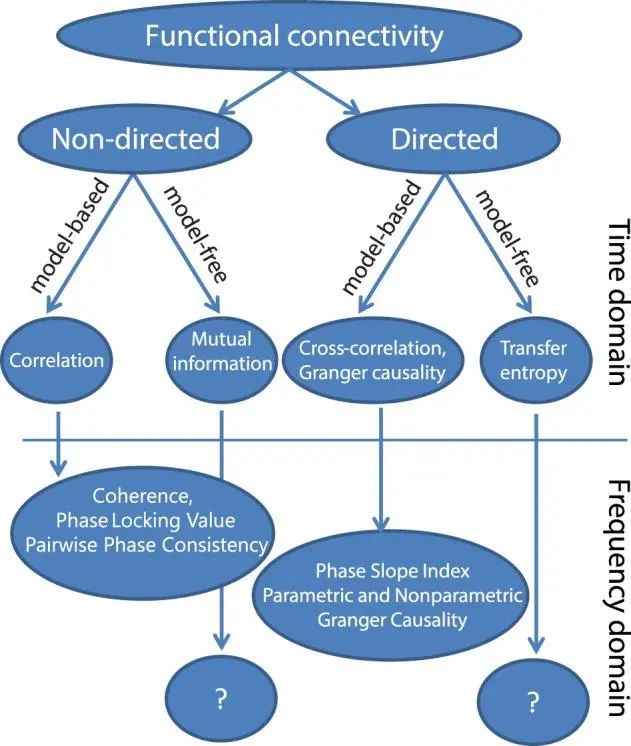
认知或知觉任务需要在功能特异的脑区网络间协调信息流,大脑可以通过改变不同脑区间同步振荡的强度、模式或频率来动态协调这一过程。上一期内容里我们介绍了将时域信号转换为频域信号的方法。本期我们进一步介绍通过估计频域功能连接指标以评估神经元间的相互作用,并用以表征生成时间序列的架构以理解大脑的工作原理。测量功能连接的方法有多种,根据有无方向和是否基于模型分为如下图所示四大类:
01
相关性(correlation )
·皮尔逊相关系数
皮尔逊相关系数(Pearson correlation coefficient)是测量两个信号x(t)和y(t)在零滞后时的时域线性相关性。计算公式如下:
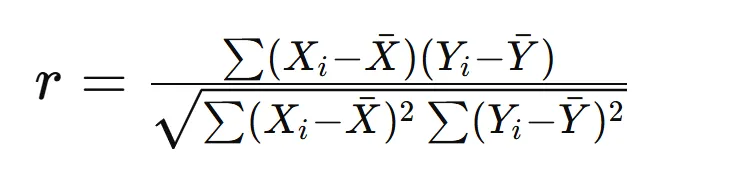
Xi和 Yi是两个变量的样本值;和 分别是变量 X和 Y的样本均值;-1≤r≤1,-1表示两个信号之间呈完全线性负相关,0表示没有线性相关性,1代表两个信号之间呈完全线性正相关。
·相干性
相干性(coherence)是用于测量两个信号之间在频域上的线性相关性指标,由两个信号的交叉功率谱除以它们各自的功率谱得到,其计算公式如下:

Pxy(f)是信号 x(t)和信号 y(t)的互功率谱(cross-power spectral density, CSPD);Pxx(f)是信号 x(t)的功率谱密度(power spectral density, PSD);Pyy(f)是信号 y(t)的功率谱密度;-1≤Cxy(f)≤1,-1表示两个信号之间呈完全线性负相关,0表示没有线性相关性,1代表两个信号之间呈完全线性正相关。
- 计算互功率谱密度的公式:Pxy(f)=X(f)⋅Y*(f)
X(f)是信号 x(t)的傅里叶变换;Y*(f)是信号 y(t)的傅里叶变换的复共轭。使用共轭复数进行相互谱计算可以保持原始信号之间的相位关系一致性,如下图所示,使用共轭复数乘积计算时结果(粉色向量)保持向量X和Y的相位差,而两个向量直接相乘(绿色向量)则没有。
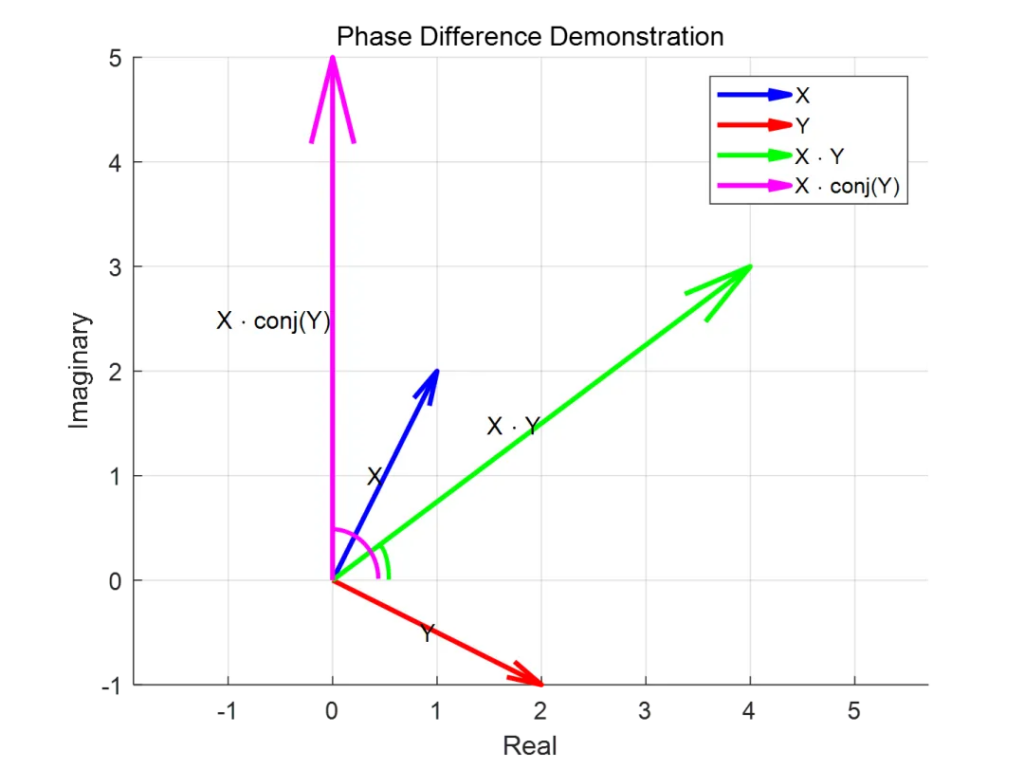
- 虚部相干性(Imaginary Coherence)
虚部相干性衡量的是信号的相位差异对它们之间相互关系的贡献。虚部相干性在某些情况下对信号之间的关系有更敏感的反映,特别是当信号之间存在非线性耦合时。计算公式如下,Im(Pxy(f))是互功率谱密度Pxy(f)的虚部。
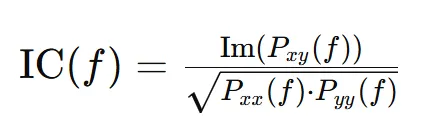
传统相干性主要关注信号的振幅关系,而虚部相干性更加注重信号的相位关系。因此,在某些情况下,虚部相干性可能提供了传统相干性所无法捕捉到的信息。
·相位同步指数
- 锁相值(Phase Locking Value, PLV)
PLV是一种用于量化信号在特定频率上的相位同步性的统计量。它测量了两个信号之间相位关系的一致性,反映了它们在某一频率上是否保持固定的相位差。计算公式如下,ϕx,n(f)和 ϕy,n(f)分别是信号 x(t)和信号 y(t)在频率 f下的相位;N是试验次数或数据块的数量。
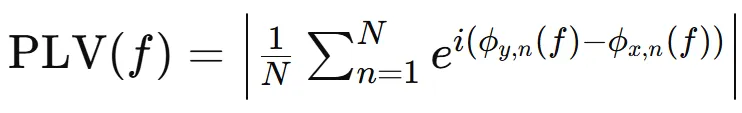
锁相计算的优点是直观易用,能够提供清晰的相位同步度量;而缺点则是易受到体积传导效应的影响,可能会虚假的增加同步值;此外,样本量的大小也会较大的影响PLV的数值。
- 配对相位一致性(Pairwise Phase Consistency, PPC)
PPC是一种新的圆形统计量,用于评估信号之间的相位同步性。与 PLV 不同,PPC 提供了一个无偏的估计量,可以更准确地反映信号之间的相位一致性。计算方式类似于 PLV,但 PPC 的定义考虑了相位的循环性质,从而避免了样本大小所带来的计算偏差。即,PPC 的计算不会因为相位跨越 0度或 2π弧度的边界而受到影响,圆形统计量能够处理这种循环性质,避免了传统线性统计方法处理相位数据时可能产生的误差。
PPC的优点是其为无偏、一致的估计量,适用于有限样本大小。而缺点是可能比 PLV 更复杂,需要更多的计算和数据处理。
下图为圆形统计量示意图:
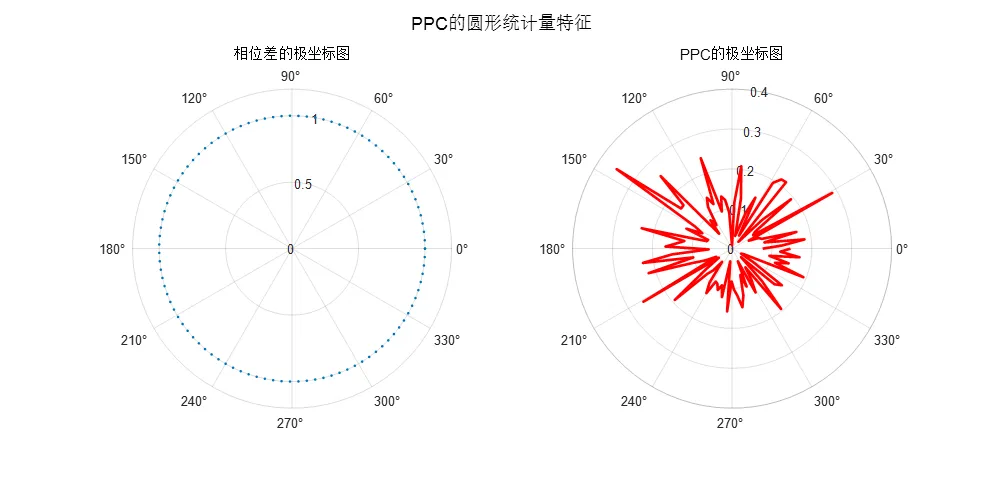
- 相位滞后指数 (Phase Lag Index, PLI)
(1) PLI是一种用于量化信号相位滞后和超前的不均匀概率的指标。它特别关注信号相位滞后和超前的非均匀分布,用于评估信号之间的相位同步性。计算公式如下,sign是符号函数,表示相位滞后和超前的方向。
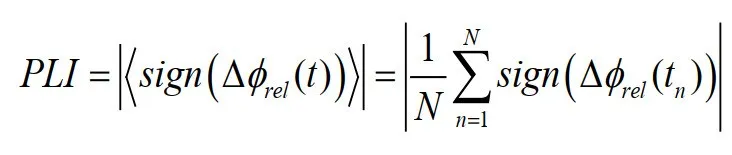
优点是PLI 对相位延迟的影响较小,更关注相位滞后和超前的非均匀性。缺点是由于 PLI 是不连续的,容易受到小扰动的影响,可能导致不稳定。
(2)加权相位滞后指数(Weighted Phase Lag Index, WPLI)是对 PLI 的改进,它通过加权来减少噪声和体积传导效应的影响。具体地,WPLI 根据相位差的虚部幅度对信号的相位滞后和超前进行加权。通过取虚部的绝对值并进行加权计算,实际上是在忽略那些相位差较小的情况,这些小的相位差可能仅仅是由随机噪声导致的而不是真正的相位一致性。在有体积传导的情况下,两个地方的信号可能会因为信号的传播而表现出相位差很小,这并不代表两个区域在功能上是同步的。
计算公式如下,Im(Pxy(f))是信号 x(t)和 y(t)互功率谱密度的虚部。
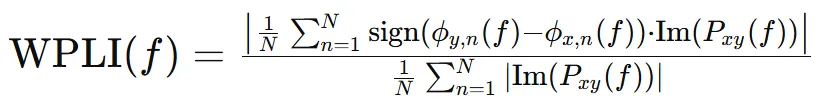
优点是对噪声和体积传导效应的敏感性降低。通过加权,WPLI 能够更好地处理体积传导效应,同时提高检测相位同步变化的能力。缺点是WPLI 的计算较为复杂,可能需要额外的计算资源。
(3)去偏加权相位滞后指数(Debiased Weighted Phase Lag Index, dWPLI)是 WPLI 的进一步改进,旨在进一步减少噪声和体积传导效应的影响。它通过去偏(de-biasing)来提高 WPLI 的准确性。考虑相位差的平方时,随机的相位差(即那些可能由噪声产生的相位差)不论是正是负,在平方之后都会变成正值。在没有一致的相位提前或延后的情况下,正负相位差的随机分布平方和可能相对较大。在计算时,对这个平方和进行了校正,从而减少了这些随机相位差对于同步性度量的贡献。
计算公式如下,BiasdWPLI是去偏估计量,旨在纠正由体积传导效应和噪声引起的偏差。
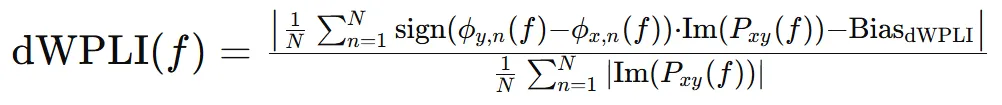
优点是通过去偏化处理,能够提供更准确的相位同步性度量,减少了由于噪声和体积传导效应造成的估计偏差。缺点是计算复杂度较高,需要进行去偏化处理。
- 相位斜率指数(Phase Slope Index, PSI)
PSL是一种用于测量两个信号之间因果关系和相位同步性的方法。PSI 基于频率域中的相位差随频率变化的斜率,尤其适用于神经科学中的脑电信号分析。PSI 通过评估信号之间的相位相干性来量化一种信号对另一种信号的驱动程度。公式如下:
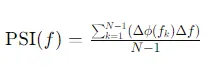
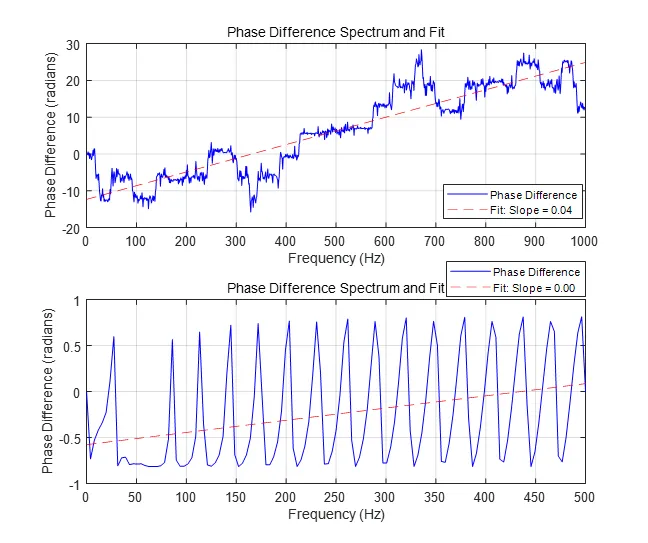
Δϕ(fk)是频率 fk处的相位差;Δf是频率分辨率;N是频率点的总数。PSI 值接近零表示没有明显的因果关系,而正值或负值分别表示信号之间存在正向或反向的因果关系。示意图如下:
02
互相关函数
互相关函数 (Cross-correlation function, XCOR)是一种用于测量两个信号或时间序列之间相似性的方法。它可以帮助分析两个信号的相位关系和时间延迟。计算公式如下,对于两个时间序列 x(t)和 y(t),互相关函数 Rxy(τ)可以定义为它们的卷积:

τ是时间延迟;x(t)和 y(t)分别是两个信号的时间函数;Rxy(τ)表示两个信号之间的相似性,随着时间延迟 τ的变化而变化。-1≤Rxy(τ)≤1。-1表示在时滞τ时,x(t)与y(t)呈完全线性负相关,0表示无线性相关性,1表示在时滞τ时,x(t)与y(t)完全线性正相关。
在计算相关性时,通过将两个时间序列相互移动(并在多个滞后时间下进行此移动),我们可以获得互相关函数。通过将互相关函数作为时间滞后的函数来评估,我们实际上考虑了数据中的时间结构。这种方法,特别是在某些情况下表现良好时,能够用于推断神经元之间的定向相互作用。
03
互信息
互信息(Mutual Information, MI)度量了两个随机变量 X和 Y之间的信息共享程度。具体来说,它衡量了一个变量所能提供的关于另一个变量的信息量。它不仅能够检测线性关系,也能够捕捉非线性关系,因此是一种比皮尔逊相关系数更全面的相互信息度量。计算公式如下:
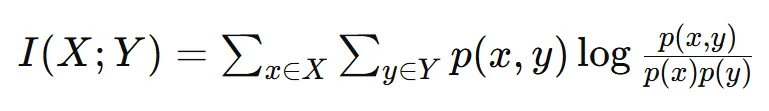
p(x,y)是随机变量 X和 Y的联合概率分布;p(x)和 p(y)分别是 X和 Y的边际概率分布;互信息度量了随机变量 X和 Y之间共享的信息量。互信息越高,说明知道 X的值能提供关于 Y的更多信息,反之亦然。
皮尔逊相关系数以及互信息本身是交互作用的非定向度量。此外,这些度量忽略了数据中的时间结构,将时间序列视为随机变量的实现。换句话说,这意味着无论时间序列是否经过随机洗牌,估计的连通性结果都是相同的。
04
格兰杰因果关系
格兰杰因果关系(Granger Causality)是一种统计检验方法,用于判断一个时间序列是否能够提供另一个时间序列未来值的信息。该方法经济学家 Clive Granger 于1969年提出,主要用于时间序列分析,评估一个变量是否有助于预测另一个变量的未来值。
03
线性格兰杰因果关系
线性格兰杰因果关系(Linear Granger Causality)是基础的格兰杰因果关系检验方法,主要用于线性模型。计算步骤:
- 回归模型:对于信号Yt建立自回归模型后,再建立包含信号Xt信息的扩展回归模型:
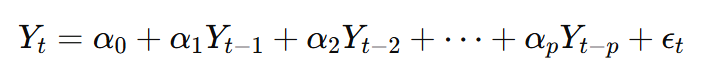
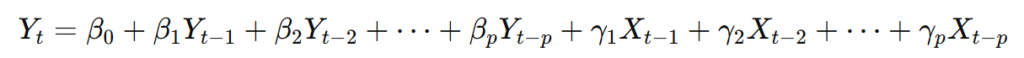
- F检验:计算残差平方和 RSS。
- 计算F统计量:
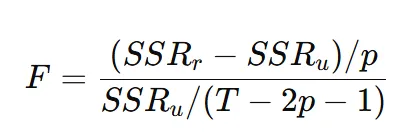
SSRr为自回归模型的残差平方和,SSRu为扩展回归模型的残差平方和,p为模型的阶数,T 为样本大小。比较F统计量与临界值,来判断是否拒绝原假设(即 X与Y之间没有“格兰杰因果性”)。
03
非线性格兰杰因果关系
非线性格兰杰因果关系(Nonlinear Granger Causality)对于非线性时间序列数据,线性格兰杰因果关系可能不适用,因此需要考虑非线性方法。例如,非线性格兰杰因果关系可以通过非线性模型如神经网络、支持向量机等进行计算,但这些方法通常较为复杂。
03
向量自回归模型
向量自回归模型(Vector Autoregression, VAR)用于多变量时间序列的格兰杰因果关系检验。VAR(p)模型L是滞后算子,Φij(L)是滞后多项式,ϵit是误差项。
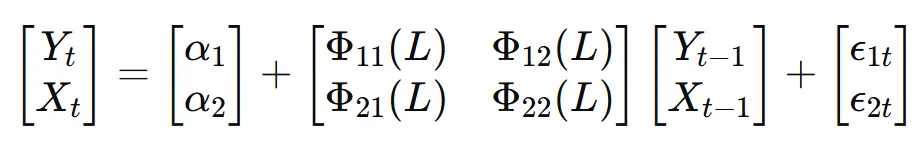
03
因果传递度量
因果传递度量(Granger Causality Measures):在某些情况下,可以使用不同的度量来估计因果关系的强度,格兰杰因果关系的标准化指标如下,这个指标表明引入 X对 Y的预测效果的提升程度。
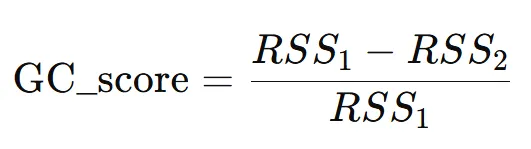
格兰杰因果关系是一种用于检验时间序列之间预测关系的统计方法,能够揭示变量之间的动态关系。虽然它不提供真实的因果关系,但对于理解时间序列数据中的依赖结构非常有用。
05
传递熵
传递熵(Transfer Entropy, TE)是一种用于测量一个时间序列对另一个时间序列的预测信息量的统计方法。与格兰杰因果关系不同,传递熵不仅能捕捉线性和非线性因果关系,还能揭示复杂的时间序列之间的信息流动。
传递熵是基于信息论的度量,用于评估在给定过去的历史数据的情况下,一个时间序列 X对另一个时间序列 Y的预测能力的提高程度。具体来说,它测量了知道 X的过去数据是否能增加对 Y的未来数据的预测精度。计算公式如下:
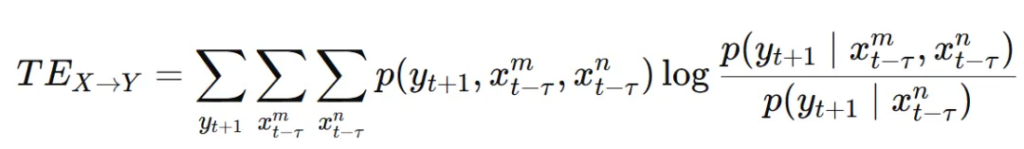
传递熵测量了时间序列 X对 Y的信息流动。在 X的过去信息帮助提高 Y未来的预测精度时,传递熵值较大。
06
FieldTrip代码示例
cfg = []; cfg.output = 'powandcsd'; cfg.method = 'mtmfft'; cfg.taper = 'dpss'; cfg.foi = 20:2:100; cfg.tapsmofrq = 5; cfg.keeptrials = 'yes'; cfg.channel = data.label; freq_csd = ft_freqanalysis(cfg, data); cfg = []; cfg.method = 'coh'; cfg.complex = 'imag'; output2 = ft_connectivityanalysis(cfg, freq_csd);
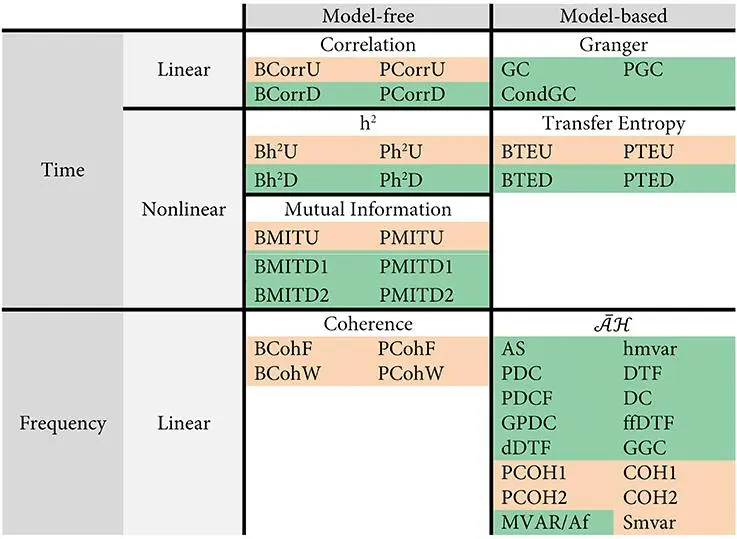
Cfg.method可选常用方法见下表
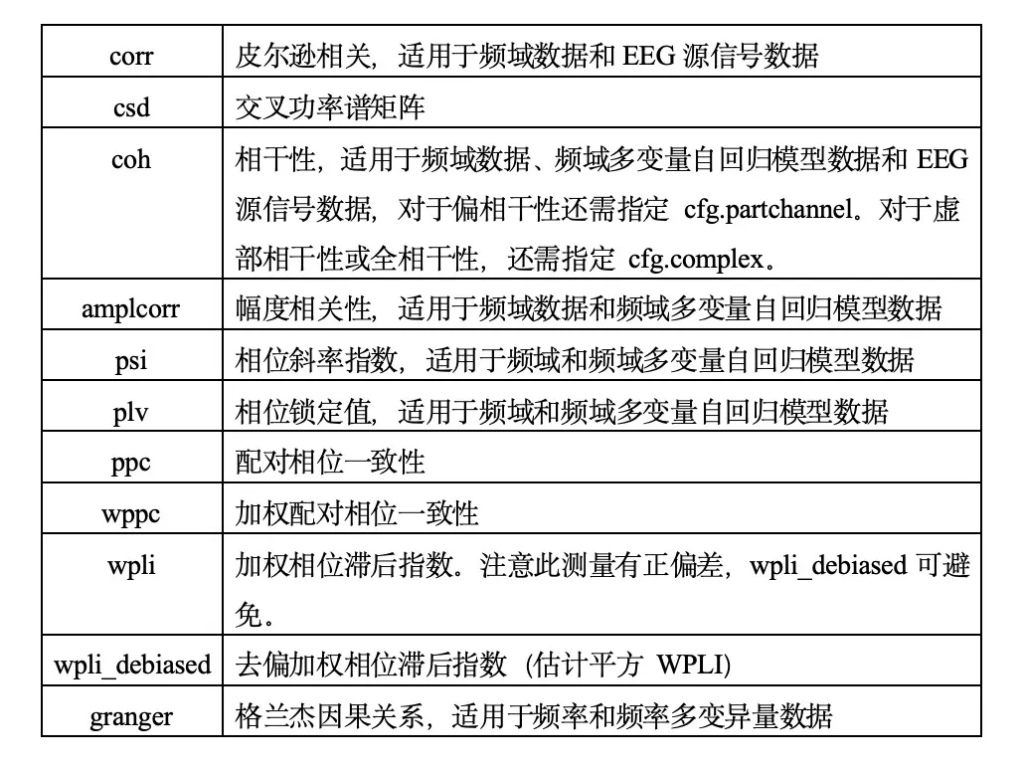
参考文献:
1.Bastos AM, Schoffelen JM. A Tutorial Review of Functional Connectivity Analysis Methods and Their Interpretational Pitfalls. Front Syst Neurosci. 2016 Jan 8;9:175. doi: 10.3389/fnsys.2015.00175. PMID: 26778976; PMCID: PMC4705224.
2.Wang HE, Bénar CG, Quilichini PP, Friston KJ, Jirsa VK, Bernard C. A systematic framework for functional connectivity measures. Front Neurosci. 2014 Dec 9;8:405. doi: 10.3389/fnins.2014.00405. PMID: 25538556; PMCID: PMC4260483.
3.Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, Hallett M. Identifying true brain interaction from EEG data using the imaginary part of coherency. Clin Neurophysiol. 2004 Oct;115(10):2292-307. doi: 10.1016/j.clinph.2004.04.029. PMID: 15351371.
4.Vinck M, van Wingerden M, Womelsdorf T, Fries P, Pennartz CM. The pairwise phase consistency: a bias-free measure of rhythmic neuronal synchronization.
Neuroimage. 2010 May 15;51(1):112-22. doi: 10.1016/j.neuroimage.2010.01.073. Epub 2010 Jan 28. PMID: 20114076.
5.Vinck M, Oostenveld R, van Wingerden M, Battaglia F, Pennartz CM. An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias. Neuroimage. 2011 Apr 15;55(4):1548-65. doi: 10.1016/j.neuroimage.2011.01.055. Epub 2011 Jan 27. PMID: 21276857.
6.Kraskov, A., Stögbauer, H., and Grassberger, P. (2004). Estimating mutual information. Phys. Rev. E 69:066138. doi: 10.1103/physreve.69.066138
7.Granger, C. W. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econ. J. Econ. Soc. 37, 424–438. doi: 10.2307/1912791
本文作者:王倩芸|复旦大学
邮箱:abelor@163.com

发表回复