Spike Sorting简介
Spike Sorting是神经科学中的一个关键技术,用于从多电极阵列记录的原始神经信号中提取和分类单个神经元的动作电位(spikes)。该过程是理解神经系统活动的基础,允许研究人员将复杂的电信号分解为独立的神经元活动。基本流程如下图所示:
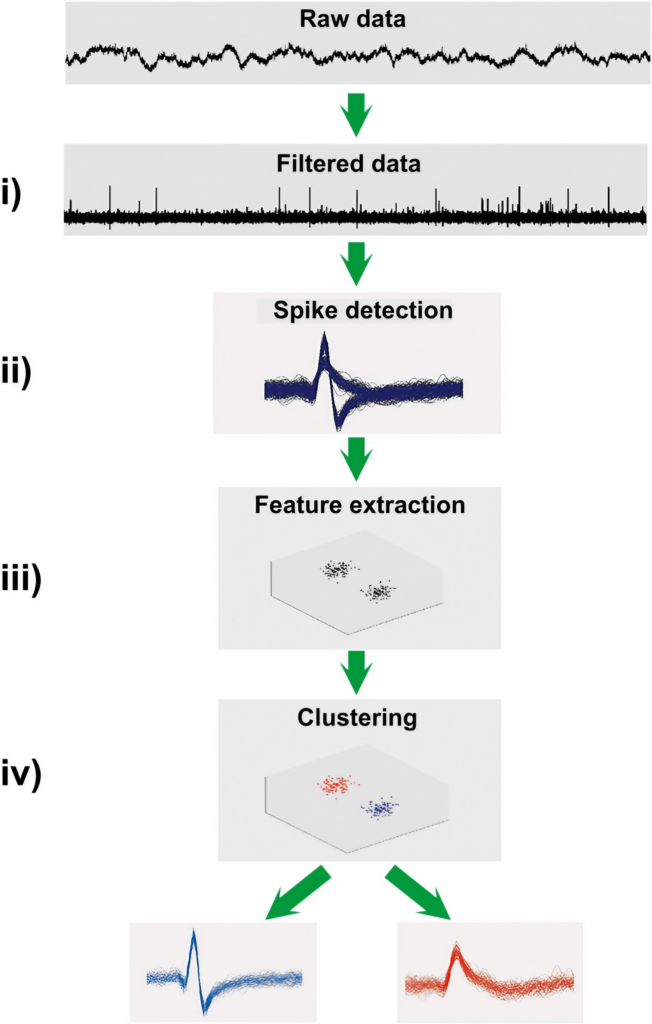
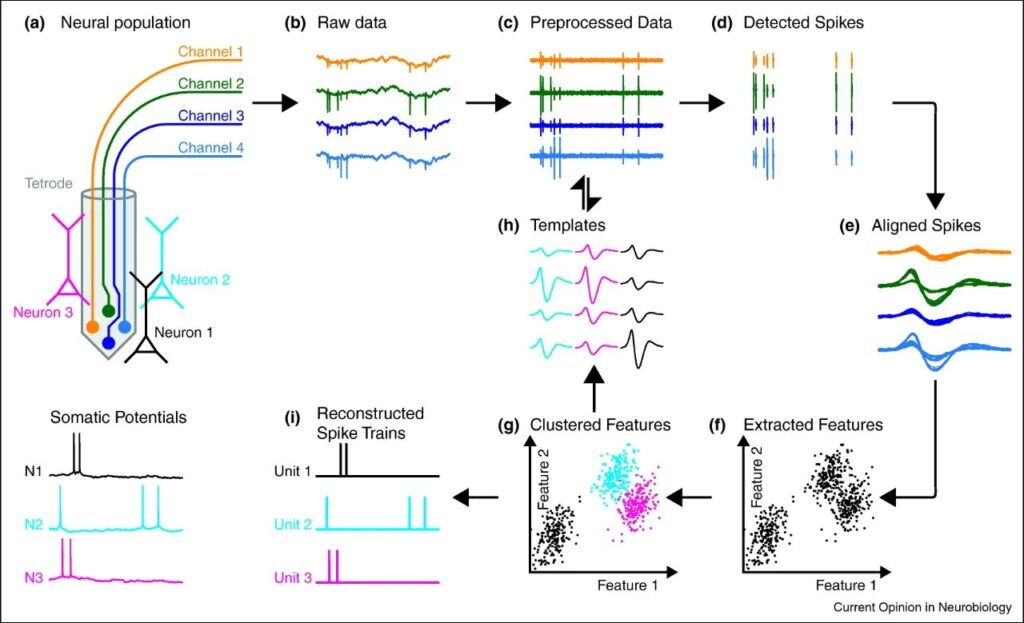
01
数据预处理 (Preprocessing)
电生理记录数据通常包含很多噪声和其他不相关的信号。因此,首先需要对数据进行预处理,包以下几个步骤:
03
共模去噪:减少或消除在所有电极上同时出现的干扰信号(共模噪声)。共模噪声可能源于电源线噪声、环境电磁干扰或实验设备的噪声,消除这些噪声有助于提高尖峰分类的准确性。常用方法有共平均参考法(Common Average Referencing, CAR)、共中位参考法(Common Median Referencing, CMR)、主成分分析(Principal Component Analysis, PCA)、自适应滤波器等。
- CAR:对所有通道每个时间点的信号求平均值,从每个通道的原始信号中减去平均值。适用于电极信号相对均匀的情况,简单且计算效率高。
- CMR:对所有通道每个时间点的信号求中位数,从每个通道的原始信号中减去该中位数。信号存在异常值或高噪声时更具鲁棒性。
- PCA:是一种多功能的统计方法,用于降维和特征提取。PCA通过将高维数据投影到低维空间,提取出能够解释数据最大方差的主成分。主成分是原始变量的若干线性组合,最大限度地解释了所有变量的方差。使用PCA方法提取主要的共模噪声成分,将这些主要成分从原始信号去除。
03
带通滤波:对输入信号进行带通滤波,通常在300 Hz到6000 Hz之间,以去除低频噪声和高频干扰。
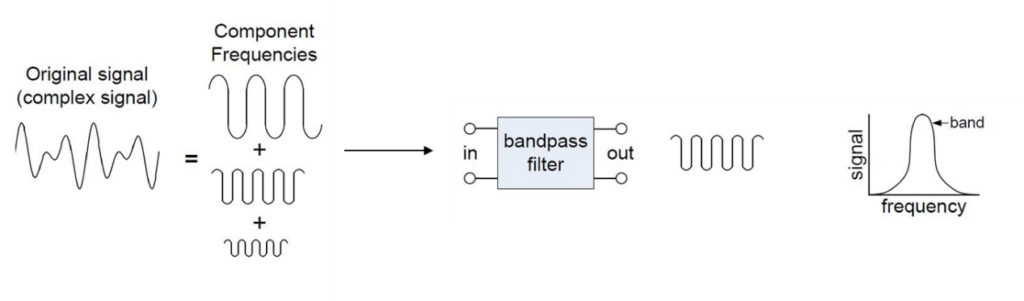
03
白化(Whitening):去除数据中的冗余信息,提高不同通道上信号的独立性和分离能力。步骤如下:
去均值:从数据集中每个数据点中减去数据的均值,使数据中心化。公式如下,X为标准化后的数据矩阵,X为m行(通道数)n列(采样点)的数据。μ是数据的均值,σ是数据的标准差。
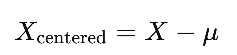
- 计算协方差矩阵:计算标准化数据的协方差矩阵C。公式如下,n代表采样点数。
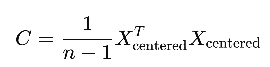
- 特征分解:对协方差矩阵进行特征值分解,得到特征值和特征向量。公式如下,E为特征向量,D为特征值。
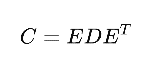
- 白化变换:应用ZCA变换,使得数据的协方差矩阵变为单位矩阵,并尽量保持原始数据结构。
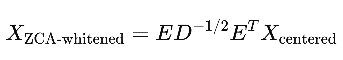
02
Spike检测 (Spike Detection)
在预处理后的数据中,检测出可能的 spike 事件。常用的方法包括:阈值检测 (Thresholding):设定一个电压阈值,当信号超过该阈值时即认为检测到了一个 spike。模板匹配:例如kilosort使用模板匹配的方法提高检测的高效性。
03
特征提取 (Feature Extraction)
对检测到的 spike 进行特征提取,将高维度的波形数据转化为低维度的特征空间,以便于后续的聚类分析。常用的特征提取方法有:主成分分析 (Principal Component Analysis, PCA):提取波形的主要成分。小波变换 (Wavelet Transform):提取波形的时频特征。
04
聚类 (Clustering)将提取的特征数据进行聚类分析,将不同神经元的 spike 分离出来。常用的聚类算法包括:
- K-means 聚类:一种简单的划分聚类方法,适应于簇数量已知且形状为球形的情况。优点是计算成本低,缺点是需要预先指定簇的数量,对初始质心敏感。
- Gaussian Mixture Model (GMM):基于概率模型的聚类方法,通过拟合多个高斯分布来进行聚类分析,可以捕捉数据的不同密度特征,适用于数据点分布为高斯分布的情况。能处理重叠分布的情况,但计算复杂。
- Density-Based Spatial Clustering of Applications with Noise (DBSCAN):是一种基于密度的聚类方法,能够很好地处理具有不同密度的数据集。它不需要预定义簇的数量,并且能够识别噪声点(即不属于任何簇的点)适合处理不同密度的簇和噪声数据。
05
验证和后处理对类结果进行验证和后处理 (Validation and Post-processing),以提高结果的准确性和稳定性。包括:
- 人工验证 (Manual Validation):人工检查和调整聚类结果。
- 自动验证 (Automatic Validation):使用不同的算法或参数进行交叉验证。
- 去除伪阳性 (False Positive Removal):去除由于噪声或其他原因造成的误检。
MountainSort简介
MountainSort是一种用于神经信号处理的峰检测和分类算法,专门用于从多通道电生理数据中提取和分类spike。应用于不同脑区数据的算法,减少用户定义的参数和建模假设,同时保持高的spike分类准确性和效率。
早期版本的Moutainsort主要在Linux系统上得到广泛的使用和支持,在MountainLab框架上使用。MountainLab通过JSON文件定义处理器和数据流,具有高度的灵活性和扩展性,可以管理复杂的数据处理流程,包括中间结果的管理和缓存。新版本使用SpikeInterface进行输入/输出和预处理,可视化更丰富,各个系统上的安装和使用较为方便。在处理高密度高通量的数据时运行速度更快,能在CPU上快速运行,更好处理时间重叠事件和漂移波形。另外,新版本语言从以C++为主转变到全使用Python。
MountainSort流程如下图所示,包括预处理、电极邻域内的聚类、跨邻域整合、拟合、聚类指标的推导以及自动注释(Cluster会根据计算出的指标被接受或拒绝)。
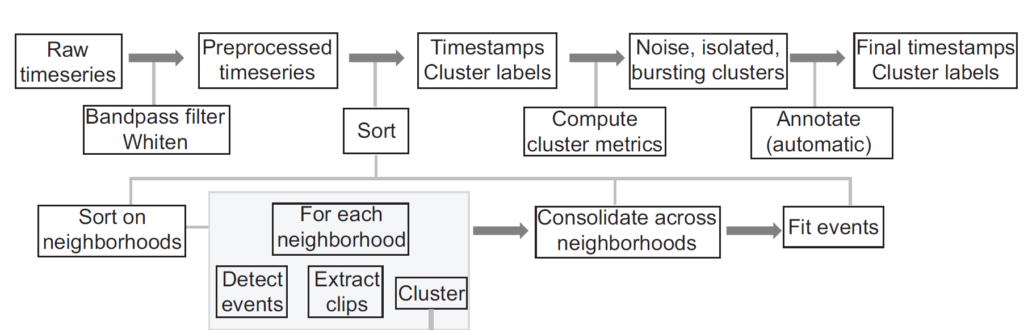
MountainSort核心算法sorting流程的核心是称为ISO-SPLIT的一种高效非参数的基于密度的聚类算法。该算法对该空间中的聚类分布只做了两个一般性假设。首先,假设每个聚类源自一个密度函数,当投影到任何线上时是单峰的,具有一个最高密度区域。其次,假设任何两个不同的聚类可以通过一个超平面分开,在其附近有一个相对较低的密度。具体的算法过程如下图所示:
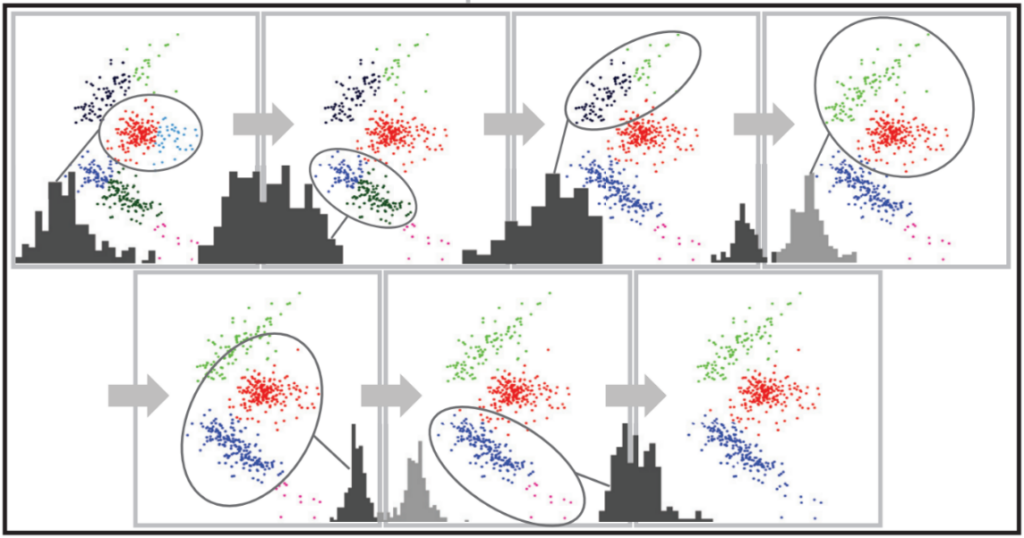
以过度聚类(细粒度的分割)开始,然后再连续的迭代将点重新分配到聚类中,直到收敛每次迭代涉及对附近聚类的成对比较。设A和B为要比较的两个聚类,首先,基于聚类的质心和经验协方差矩阵将A和B的点投影到一条最佳区分线,即将聚类的多维特征投影到一维上。接下来,执行一个统计检验,以确定投影得到的一维样本是否是单峰。如果单峰性假设被拒绝,则根据ISO-CUT确定的最佳切割点,将数据点在A和B之间重新分配。否则,如果单峰性假设被接受,则两个聚类合并。ISO-CUT算法(ISO-SPLIT中的核心操作)是一种非参数方法,用于测试一维样本是否来自单峰分布,并确定用于聚类的最佳切割点。类似于Hartigan检验,但区别是Hartigan检验只是接受/拒绝单峰假设的一个标准,而ISO-CUT还返回一个最佳切割点。其次,ISO-CUT使用最大似然单峰近似来处理数据,可以通过修改后的单调回归高效地评估。第三,ISO-CUT能处理一个稀疏簇邻近一个非常密集的簇的情况,而Hartigan检验不适用。ISO-CUT算法首先对一维数据点排序,并计算样本的最大似然单峰拟合,通过“上-下单调回归”获得拟合的密度函数。然后计算修改后的Kolmogorov-Smirnov统计量来衡量经验累积分布函数与单峰近似的接近程度。如果统计量超过阈值,则拒绝单峰性假设。在这种情况下,ISO-SPLIT通过“下-上单调回归”找到两个模式之间的最佳切割点,以非参数方式获得最佳切割点,无需密度估计。附录:MountainSort的使用代码:链接:https://pan.baidu.com/s/1fr4YCMQHj5HI4-oxwi0rQw?pwd=t4rf提取码:t4rf
参考文献:
[1] Rey HG, Pedreira C, Quian Quiroga R. Past, present and future of spike sorting techniques. Brain Res Bull. 2015 Oct;119(Pt B):106-17. doi: 10.1016/j.brainresbull.2015.04.007. Epub 2015 Apr 27. PMID: 25931392; PMCID: PMC4674014.
[2] Einevoll GT, Franke F, Hagen E, Pouzat C, Harris KD. Towards reliable spike-train recordings from thousands of neurons with multielectrodes. Curr Opin Neurobiol. 2012 Feb;22(1):11-7. doi: 10.1016/j.conb.2011.10.001. Epub 2011 Oct 22. PMID: 22023727; PMCID: PMC3314330.
[3] Greenacre, M., Groenen, P.J.F., Hastie, T. et al. Principal component analysis. Nat Rev Methods Primers 2, 100 (2022).
[4] Kessy, A., Lewin, A., & Strimmer, K. (2018). Optimal whitening and decorrelation. The American Statistician, 72(4), 309-314.
[5] Chung JE, Magland JF, Barnett AH, Tolosa VM, Tooker AC, Lee KY, Shah KG, Felix SH, Frank LM, Greengard LF. A Fully Automated Approach to Spike Sorting. Neuron. 2017 Sep 13;95(6):1381-1394.e6. doi: 10.1016/j.neuron.2017.08.030. PMID: 28910621; PMCID: PMC5743236.
本文作者:王倩芸|复旦大学 邮箱:abelor@163.com欢 迎 沟 通 交 流 !

发表回复